Forskjell mellom versjoner av «Midtlivskrise»
| (8 mellomliggende revisjoner av samme bruker vises ikke) | |||
| Linje 15: | Linje 15: | ||
Matematisk kan dette uttrykkes som: | Matematisk kan dette uttrykkes som: | ||
| − | < | + | <math> |
I=\frac{k}{t} | I=\frac{k}{t} | ||
| − | </ | + | </math> |
der ''t'' er tiden siden fødsel, ''k'' er en proporsjonalitetskonstant, og ''I'' er opplevelsesintensiteten. | der ''t'' er tiden siden fødsel, ''k'' er en proporsjonalitetskonstant, og ''I'' er opplevelsesintensiteten. | ||
| Linje 23: | Linje 23: | ||
Opplevelsesintensiteten er som nevnt et mål på antall nye opplevelser per tidsenhet, altså den deriverte av antall nye opplevelser, ''y''. | Opplevelsesintensiteten er som nevnt et mål på antall nye opplevelser per tidsenhet, altså den deriverte av antall nye opplevelser, ''y''. | ||
| − | < | + | <math> |
\frac{dy}{dt}=I | \frac{dy}{dt}=I | ||
| − | </ | + | </math> |
| − | < | + | <math> |
\frac{dy}{dt}=\frac{k}{t} | \frac{dy}{dt}=\frac{k}{t} | ||
| − | </ | + | </math> |
For å finne et direkte uttrykk for opplevelsene, integrerer vi på begge sider og får | For å finne et direkte uttrykk for opplevelsene, integrerer vi på begge sider og får | ||
| − | < | + | <math> |
y=k\:\mathrm{ln}\:t+c | y=k\:\mathrm{ln}\:t+c | ||
| − | </ | + | </math> |
der ''c'' er en integrasjonskonstant. | der ''c'' er en integrasjonskonstant. | ||
| Linje 43: | Linje 43: | ||
[[Image:Alder0.png|x300px|alt=Opplevelsesintensitet|Opplevelsesintensitet]] | [[Image:Alder0.png|x300px|alt=Opplevelsesintensitet|Opplevelsesintensitet]] | ||
| − | De fleste mennesker har ingen minner fra de første årene av livet, og som en følge av dette vil ikke denne tiden påvirke midtlivsberegningene. Grensen for begynnende barneminner ligger oftest et sted mellom 2 og 5 år, med 3,5 som gjennomsnittlig verdi. Det er derfor tilforlatelig å innføre konvensjonen at opplevd alder er null ved første minne, eller: | + | De fleste mennesker har ingen minner fra de første årene av livet, og som en følge av dette vil ikke denne tiden påvirke midtlivsberegningene. Grensen for begynnende barneminner ligger oftest et sted mellom 2 og 5 år, med 3,5 som gjennomsnittlig verdi. Det er vanlig å regne 3,5 år som alderen for første minne. Det er derfor tilforlatelig å innføre konvensjonen at opplevd alder er null ved første minne, eller: |
| − | < | + | <math> |
y\left(t_{min}\right)=0 | y\left(t_{min}\right)=0 | ||
| − | </ | + | </math> |
som gir at | som gir at | ||
| − | < | + | <math> |
c=-k\,\mathrm{ln}\, t_{min} | c=-k\,\mathrm{ln}\, t_{min} | ||
| − | </ | + | </math> , eller: |
| − | < | + | <math> |
y=k\,\mathrm{ln}\,\frac{t}{t_{min}} | y=k\,\mathrm{ln}\,\frac{t}{t_{min}} | ||
| − | </ | + | </math> |
For skalering innfører vi at antall opplevelser ved livets slutt er 1. | For skalering innfører vi at antall opplevelser ved livets slutt er 1. | ||
| − | < | + | <math> |
y\left(t_{max}\right)=1 | y\left(t_{max}\right)=1 | ||
| − | </ | + | </math> |
som gir at | som gir at | ||
| − | < | + | <math> |
k=\frac{1}{\mathrm{ln}\,\frac{t_{max}}{t_{min}}} | k=\frac{1}{\mathrm{ln}\,\frac{t_{max}}{t_{min}}} | ||
| − | </ | + | </math> , eller: |
| − | < | + | <math> |
y=\frac{\mathrm{ln}\frac{t}{t_{min}}} | y=\frac{\mathrm{ln}\frac{t}{t_{min}}} | ||
{\mathrm{ln}\frac{t_{max}}{t_{min}}} | {\mathrm{ln}\frac{t_{max}}{t_{min}}} | ||
| − | </ | + | </math> |
Man er midtveis i livet når antall opplevelser er halvparten av det det vil bli i løpet av livet, altså når arealet under opplevelsesintensitetskurven er halvparten av det totale arealet under kurven, som vist i figuren under. | Man er midtveis i livet når antall opplevelser er halvparten av det det vil bli i løpet av livet, altså når arealet under opplevelsesintensitetskurven er halvparten av det totale arealet under kurven, som vist i figuren under. | ||
| Linje 88: | Linje 88: | ||
| − | Analytisk kan vi finne et uttrykk for det | + | Analytisk kan vi finne et uttrykk for det harmoniske midtpunktet slik: |
| − | < | + | <math> |
y_{1/2}=\frac{\mathrm{ln}\frac{t_{1/2}}{t_{min}}} | y_{1/2}=\frac{\mathrm{ln}\frac{t_{1/2}}{t_{min}}} | ||
{\mathrm{ln}\frac{t_{max}}{t_{min}}}=\frac{t_{max}}{2} | {\mathrm{ln}\frac{t_{max}}{t_{min}}}=\frac{t_{max}}{2} | ||
| − | </ | + | </math> |
som gir | som gir | ||
| − | < | + | <math> |
t_{1/2}=\sqrt{t_{max}t_{min}} | t_{1/2}=\sqrt{t_{max}t_{min}} | ||
| − | </ | + | </math> |
Forventet levealder i Norge i dag er omtrent 80 år. For de ulike verdiene av ''t<sub>min</sub>'', henholdsvis 2, 3.5 og 5 år, gir dette 12.6, 16.7 og 20 år som midtlivsalderen. | Forventet levealder i Norge i dag er omtrent 80 år. For de ulike verdiene av ''t<sub>min</sub>'', henholdsvis 2, 3.5 og 5 år, gir dette 12.6, 16.7 og 20 år som midtlivsalderen. | ||
| + | |||
| + | [[Image:Alder3.png|x300px|alt=Harmonisk midtlivsalder|Harmonisk midtlivsalder]] | ||
Hvis ditt første minne var da du var tre og et halvt år, og du er over 17 år i dag, er livet på [[hell]]. | Hvis ditt første minne var da du var tre og et halvt år, og du er over 17 år i dag, er livet på [[hell]]. | ||
| − | == | + | == Eksponentmidtlivskrise == |
| − | Ifølge denne modellen | + | Ifølge denne modellen er akselerasjonen i tidens hastighet skapt av inflasjon. Årsaken til dette er fremveksten av [[tidsbank]]er som gir rente på tidsinnskudd, slik at tiden blir mindre verdt etter hvert som den (tiden) går. Opplevd tidshastighet kan modelleres med følgende modell: |
| − | |||
| − | |||
| − | < | + | <math>\frac{dy}{dt}=(1+r)^{-t}</math>, der ''r'' er tidens inflasjonsrate. |
Ved å integrere får vi et uttrykk for tidens hastighet som en funksjon av tid: | Ved å integrere får vi et uttrykk for tidens hastighet som en funksjon av tid: | ||
| − | < | + | <math>y=-\frac{k^{t}}{ln \left(k \right) } + c</math>, der c er en integrasjonskonstant og ''k'' = 1 + ''r''. |
Vi setter ''y''(0) = 0 og får | Vi setter ''y''(0) = 0 og får | ||
| − | < | + | <math>y=\frac{1-k^{-t}}{ln \left( k \right) }</math>. |
| − | Som tidligere oppstår midlivskrisa når opplevd alder passerer opplevd alder ved livets slutt: | + | Som tidligere oppstår midlivskrisa når opplevd alder passerer halvparten av opplevd alder ved livets slutt: |
| − | < | + | <math>y \left( t_{1/2} \right) = \frac{1}{2} \cdot y(t_{max})</math> |
| − | < | + | <math>\frac{1-k^{-t_{1/2}}}{ln \left( k \right) }=\frac{1}{2} \cdot \frac{1-k^{-t_{max}}}{ln \left( k \right) }</math> |
Ved å løse for ''t<sub>1/2</sub>'' får vi | Ved å løse for ''t<sub>1/2</sub>'' får vi | ||
| − | < | + | <math>t_{1/2} = - \frac{ln \left( 1 - \frac{1}{2} \cdot \left( 1 - k^{-t_{max}} \right) \right)}{ln \left( k \right)}</math>. |
| + | |||
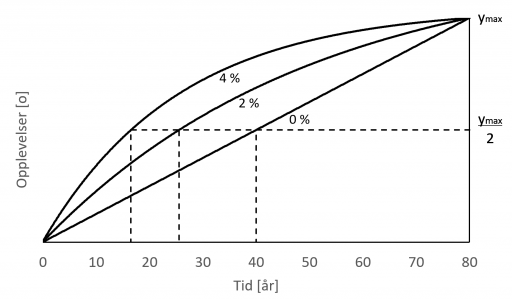
| + | I motsetning til den andre modellen er ikke eksponentmodellen basert på opplevelser og minner, og derfor har man ikke [[problem]]et med å definere et startpunkt. Men siden modellen er basert på inflasjon, forutsetter den en inflasjonsrate. Hvis man setter inflasjonsraten til 0 %, får man det aritmetiske gjennomsnittet, 40 år ved en forventet levealder på 80 år. 1 % inflasjon gir eksponentmidtlivskrise ved 32 år, 2 % ved 26 år, 3 % ved 20 år og 4 % ved 17 år. Det er vanlig å regne 4 % inflasjon. | ||
| − | + | [[Image:Alder4.png|x300px|alt=Eksponentiell midtlivsalder|Eksponentiell midtlivsalder]] | |
Modellen forteller oss at inflasjonen gjør at tiden blir mindre og mindre verdt etter som man blir eldre, slik at verdien av de første leveårene raskt overgår verdien av hele resten av livet. | Modellen forteller oss at inflasjonen gjør at tiden blir mindre og mindre verdt etter som man blir eldre, slik at verdien av de første leveårene raskt overgår verdien av hele resten av livet. | ||
| Linje 139: | Linje 141: | ||
Aldersforårsaket [[tidsdilatasjon]] påvirker også lengden av muntlig fortalte historier. Hendelser i fortiden oppleves som å ha vart lenger enn om de hadde skjedd i nåtiden, og følgelig vil historien bli lengre. | Aldersforårsaket [[tidsdilatasjon]] påvirker også lengden av muntlig fortalte historier. Hendelser i fortiden oppleves som å ha vart lenger enn om de hadde skjedd i nåtiden, og følgelig vil historien bli lengre. | ||
| − | Eksempelvis vil en 80 år gammel person som forteller en historie fra vedkommende var 40 år, bruke dobbelt så lang tid på å fortelle historien som om den tilsvarende hendelsen skjedde på fortellertidspunktet. Tilsvarende vil en 20 år yngre person som opplevde den samme hendelsen bruke tre ganger | + | Eksempelvis vil en 80 år gammel person som forteller en historie fra vedkommende var 40 år, bruke dobbelt så lang tid på å fortelle historien som om den tilsvarende hendelsen skjedde på fortellertidspunktet. Tilsvarende vil en 20 år yngre person som opplevde den samme hendelsen bruke tre ganger så lang tid som om hendelsen skjedde på fortellertidspunktet. |
Prosessen forklarer også hvorfor verden oppleves som mindre i dag enn for 60 år siden, og hvorfor det er slik at jo eldre du er, jo lengre skolevei hadde du som barn. | Prosessen forklarer også hvorfor verden oppleves som mindre i dag enn for 60 år siden, og hvorfor det er slik at jo eldre du er, jo lengre skolevei hadde du som barn. | ||
[[Kategori: Matematikk]] | [[Kategori: Matematikk]] | ||
| + | |||
| + | == Økt livslengde == | ||
| + | Mange drømmer om å få et langt liv. Men modellen over viser at dette ikke har så mye for seg. Med standardantakelsene om 3,5 år ved første minne, har man opplevd 80 % av hva man kan forvente i et liv på 80 år etter bare 43 år. Tilsvarende tall for modell 2 med 4 % inflasjon er 37 år. For å opplevd livslengde med bare 10 % må man ifølge modell 1 bli 110 år gammel, og for å øke med 20 % må man faktisk bli 150 år. | ||
Nåværende revisjon fra 13. mar. 2023 kl. 10:54
Du trodde kanskje at midtlivskrise var den vanskelige perioden mange menn opplever en gang i alderen 40-60 år? Nei, gå og legg deg, du gamlefar. Midtlivskrisa skjer i tenårene.
Innledning
At tiden ikke er lineær, er en kjent sak. Dette er et resultat av relativitetsteorien og delvis en følge av kroppens økte masse gjennom livet og radioaktiv degradering. På grunn av dette er det ikke fornuftig å snakke om en midtlivskrise ved livets aritmetiske middelpunkt.
Det finnes to hovedmodeller for å forklare midtlivskrisa. Disse baserer seg på to ulike forklaringsmodeller for hvorfor tidens hastighet virker som den akselererer.
Harmonisk midtlivskrise
Ifølge denne modellen måles alle opplevelser i livet opp mot det du allerede har opplevd, og derfor føles tiden mye raskere når du er 50 enn når du er 5, fordi det siste året bare er en brøkdel av alt du tidligere har opplevd. Antall nye opplevelser blir nødvendigvis sjeldnere etter som de fleste opplevelser allerede er opplevd før.
Opplevelsesintensiteten er et mål på frekvensen av nye opplevelser i livet. Denne antas å være proporsjonal med opplevd følelse av tidens hastighet, og vi kan derfor bruke antall nye opplevelser i livet som et indirekte mål på opplevd alder.
Vi antar at opplevelsesintensiteten er omvendt proporsjonal med alderen.
Matematisk kan dette uttrykkes som\[ I=\frac{k}{t} \]
der t er tiden siden fødsel, k er en proporsjonalitetskonstant, og I er opplevelsesintensiteten.
Opplevelsesintensiteten er som nevnt et mål på antall nye opplevelser per tidsenhet, altså den deriverte av antall nye opplevelser, y.
\( \frac{dy}{dt}=I \)
\( \frac{dy}{dt}=\frac{k}{t} \)
For å finne et direkte uttrykk for opplevelsene, integrerer vi på begge sider og får
\( y=k\:\mathrm{ln}\:t+c \)
der c er en integrasjonskonstant.
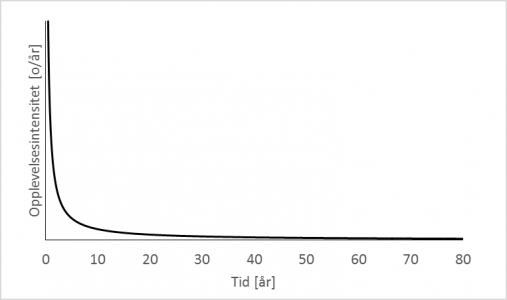
Figuren under viser opplevelsesintensiteten gjennom hele livet, på en dimensjonsløs skala. Vi ser at opplevelsesintensiteten går mot uendelig ved t=0, og synker stadig nedover mot 0 etter som t øker. Arealet under kurven er antall opplevelser.
De fleste mennesker har ingen minner fra de første årene av livet, og som en følge av dette vil ikke denne tiden påvirke midtlivsberegningene. Grensen for begynnende barneminner ligger oftest et sted mellom 2 og 5 år, med 3,5 som gjennomsnittlig verdi. Det er vanlig å regne 3,5 år som alderen for første minne. Det er derfor tilforlatelig å innføre konvensjonen at opplevd alder er null ved første minne, eller\[ y\left(t_{min}\right)=0 \]
som gir at
\( c=-k\,\mathrm{ln}\, t_{min} \) , eller\[ y=k\,\mathrm{ln}\,\frac{t}{t_{min}} \]
For skalering innfører vi at antall opplevelser ved livets slutt er 1.
\( y\left(t_{max}\right)=1 \)
som gir at
\( k=\frac{1}{\mathrm{ln}\,\frac{t_{max}}{t_{min}}} \) , eller\[ y=\frac{\mathrm{ln}\frac{t}{t_{min}}} {\mathrm{ln}\frac{t_{max}}{t_{min}}} \]
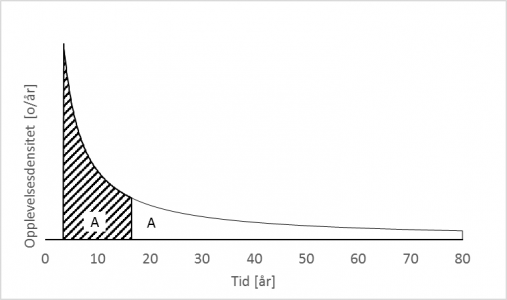
Man er midtveis i livet når antall opplevelser er halvparten av det det vil bli i løpet av livet, altså når arealet under opplevelsesintensitetskurven er halvparten av det totale arealet under kurven, som vist i figuren under.
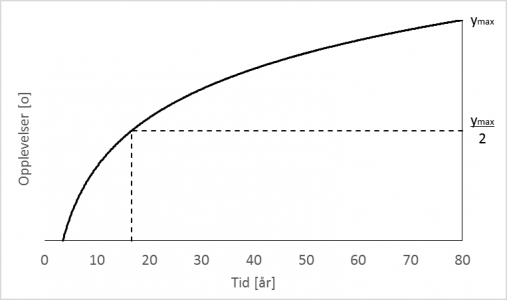
På opplevelseskurven kan man lese av midtlivstidspunktet direkte der kurven krysser ymax/2-linjen.
Analytisk kan vi finne et uttrykk for det harmoniske midtpunktet slik\[
y_{1/2}=\frac{\mathrm{ln}\frac{t_{1/2}}{t_{min}}}
{\mathrm{ln}\frac{t_{max}}{t_{min}}}=\frac{t_{max}}{2}
\]
som gir
\( t_{1/2}=\sqrt{t_{max}t_{min}} \)
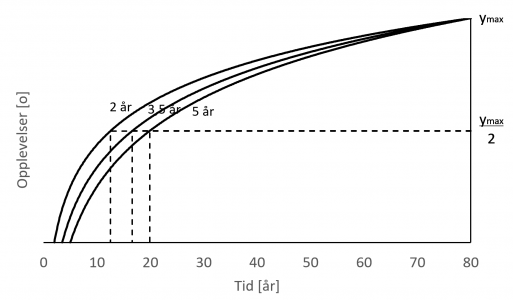
Forventet levealder i Norge i dag er omtrent 80 år. For de ulike verdiene av tmin, henholdsvis 2, 3.5 og 5 år, gir dette 12.6, 16.7 og 20 år som midtlivsalderen.
Hvis ditt første minne var da du var tre og et halvt år, og du er over 17 år i dag, er livet på hell.
Eksponentmidtlivskrise
Ifølge denne modellen er akselerasjonen i tidens hastighet skapt av inflasjon. Årsaken til dette er fremveksten av tidsbanker som gir rente på tidsinnskudd, slik at tiden blir mindre verdt etter hvert som den (tiden) går. Opplevd tidshastighet kan modelleres med følgende modell\[\frac{dy}{dt}=(1+r)^{-t}\], der r er tidens inflasjonsrate.
Ved å integrere får vi et uttrykk for tidens hastighet som en funksjon av tid\[y=-\frac{k^{t}}{ln \left(k \right) } + c\], der c er en integrasjonskonstant og k = 1 + r.
Vi setter y(0) = 0 og får
\(y=\frac{1-k^{-t}}{ln \left( k \right) }\).
Som tidligere oppstår midlivskrisa når opplevd alder passerer halvparten av opplevd alder ved livets slutt\[y \left( t_{1/2} \right) = \frac{1}{2} \cdot y(t_{max})\]
\(\frac{1-k^{-t_{1/2}}}{ln \left( k \right) }=\frac{1}{2} \cdot \frac{1-k^{-t_{max}}}{ln \left( k \right) }\)
Ved å løse for t1/2 får vi
\(t_{1/2} = - \frac{ln \left( 1 - \frac{1}{2} \cdot \left( 1 - k^{-t_{max}} \right) \right)}{ln \left( k \right)}\).
I motsetning til den andre modellen er ikke eksponentmodellen basert på opplevelser og minner, og derfor har man ikke problemet med å definere et startpunkt. Men siden modellen er basert på inflasjon, forutsetter den en inflasjonsrate. Hvis man setter inflasjonsraten til 0 %, får man det aritmetiske gjennomsnittet, 40 år ved en forventet levealder på 80 år. 1 % inflasjon gir eksponentmidtlivskrise ved 32 år, 2 % ved 26 år, 3 % ved 20 år og 4 % ved 17 år. Det er vanlig å regne 4 % inflasjon.
Modellen forteller oss at inflasjonen gjør at tiden blir mindre og mindre verdt etter som man blir eldre, slik at verdien av de første leveårene raskt overgår verdien av hele resten av livet.
Historiefortelling
Aldersforårsaket tidsdilatasjon påvirker også lengden av muntlig fortalte historier. Hendelser i fortiden oppleves som å ha vart lenger enn om de hadde skjedd i nåtiden, og følgelig vil historien bli lengre.
Eksempelvis vil en 80 år gammel person som forteller en historie fra vedkommende var 40 år, bruke dobbelt så lang tid på å fortelle historien som om den tilsvarende hendelsen skjedde på fortellertidspunktet. Tilsvarende vil en 20 år yngre person som opplevde den samme hendelsen bruke tre ganger så lang tid som om hendelsen skjedde på fortellertidspunktet.
Prosessen forklarer også hvorfor verden oppleves som mindre i dag enn for 60 år siden, og hvorfor det er slik at jo eldre du er, jo lengre skolevei hadde du som barn.
Økt livslengde
Mange drømmer om å få et langt liv. Men modellen over viser at dette ikke har så mye for seg. Med standardantakelsene om 3,5 år ved første minne, har man opplevd 80 % av hva man kan forvente i et liv på 80 år etter bare 43 år. Tilsvarende tall for modell 2 med 4 % inflasjon er 37 år. For å opplevd livslengde med bare 10 % må man ifølge modell 1 bli 110 år gammel, og for å øke med 20 % må man faktisk bli 150 år.