Midtlivskrise

Du trodde kanskje at midtlivskrise var den vanskelige perioden mange menn opplever en gang i alderen 40-60 år? Nei, gå og legg deg, du gamlefar. Midtlivskrisa skjer i tenårene.

Geometrisk midlivskrise

At tiden ikke er lineær, er en kjent sak. Dette er et resultat av relativitetsteorien og delvis en følge av kroppens økte masse gjennom livet og radioaktiv degradering. På grunn av dette er det ikke fornuftig å snakke om en midtlivskrise ved livets aritmetiske middelpunkt. I virkeligheten går tiden raskere med alderen, og det kan vises ^{[trenger referanse]} at tiden er omvent proporsjonal med alderen. Dette kan uttrykkes matematisk som

<m> \frac{dy}{dt}=\frac{k}{t} </m>

der t er tiden siden fødsel, k er en proporsjonalitetskonstant, og y er den opplevde alderen. Integrert gir dette

<m> y=k\:\mathrm{ln}\:t+c </m>

der c er en integrasjonskonstant.

De fleste mennesker har ingen minner fra de første årene av livet, og som en følge av dette vil ikke denne tiden påvirke midtlivsberegningene. Grensen for begynnende barneminner ligger oftest et sted mellom 2 og 5 år, med 3,5 som gjennomsnittlig verdi. Det er derfor tilforlatelig å innføre konvensjonen at opplevd alder er null ved første minne, eller

<m> y\left(t_{min}\right)=0 </m>

som gir at

<m> c=-k\,\mathrm{ln}\, t_{min} </m> , eller

<m> y=k\,\mathrm{ln}\,\frac{t}{t_{min}} </m>

Mot slutten av livet er det naturlig å anta at opplevd alder stabiliserer seg mot reell alder, og vi innfører konvensjonen

<m> y\left(t_{max}\right)=t_{max} </m>

som gir at

<m> k=\frac{t_{max}}{\mathrm{ln}\,t_{max}-\mathrm{ln}\,t_{min}} </m> , eller

<m> y=t_{max}\frac{\mathrm{ln}\,t-\mathrm{ln}\,t_{min}}{\mathrm{ln}\,t_{max}-\mathrm{ln}\,t_{min}} </m>

Forventet levealder i Norge i dag er omtrent 80 år, og man er midt i livet når opplevd alder er halvparten av opplevd alder ved slutten av livet, eller

<m> y_{1/2}=t_{max}\frac{\mathrm{ln}\,t_{1/2}-\mathrm{ln}\,t_{min}}{\mathrm{ln}\,t_{max}-\mathrm{ln}\,t_{min}}=\frac{t_{max}}{2} </m>

som gir

<m> t_{1/2}=\sqrt{t_{max}t_{min}} </m>

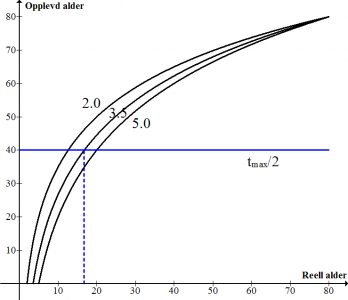
For de ulike verdiene av t_min, henholdsvis 2, 3.5 og 5 år, gir dette 12,6 16,7 og 20 år som midtlivsalderen.