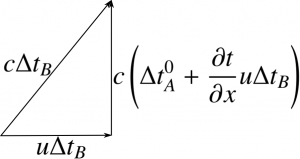Forskjell mellom versjoner av «Tidsdilatasjon»
m |
|||
| (3 mellomliggende revisjoner av samme bruker vises ikke) | |||
| Linje 1: | Linje 1: | ||
| − | <onlyinclude> | + | <onlyinclude>Du trodde kanskje at '''tidsdilatasjon''' er et fenomen beskrevet av relativitetsteorien som garanterer et hastighetssupremum satt av lyshastigheten ved at selve tiden oppfattet av observatører i forskjellige referansesystemer er forskjellige. |
| − | Du trodde kanskje at '''tidsdilatasjon''' er et fenomen beskrevet av relativitetsteorien som garanterer et hastighetssupremum satt av lyshastigheten ved at selve tiden oppfattet av observatører i forskjellige referansesystemer er forskjellige. | + | Selv om du kanskje akkurat denne gangen begynner å nærme deg snevet av en valid tankerekke, er prinsippene du bygger på noget mangelfulle.</onlyinclude> |
| − | Selv om du kanskje akkurat denne gangen begynner å nærme deg snevet av en valid tankerekke, er prinsippene du bygger på noget mangelfulle. | ||
| − | </onlyinclude> | ||
== Tidsdilatasjon for translatorisk bevegelse uten akselerasjon som presentert av Albert Einstein == | == Tidsdilatasjon for translatorisk bevegelse uten akselerasjon som presentert av Albert Einstein == | ||
| Linje 10: | Linje 8: | ||
# Bevegelsen til et legeme er ''relativ'' til det referansesystem bevegelsen observeres fra. | # Bevegelsen til et legeme er ''relativ'' til det referansesystem bevegelsen observeres fra. | ||
| − | # Lysets hastighet (< | + | # Lysets hastighet (<math>c \approx 3\cdot10^{8}</math> <sup>m</sup>/<sub>s</sub>) er absolutt, uavhengig av referansesystem. |
[[Albert Einstein]] nyttiggjorde seg av tog for å illustrere dette konseptet. En klokke, senere kjent som ''Einsteins klokke'', ble introdusert. Denne klokken regner et "tikk" som den tiden klokken bruker på å sende et foton en vertikal distanse mellom to sensorer. | [[Albert Einstein]] nyttiggjorde seg av tog for å illustrere dette konseptet. En klokke, senere kjent som ''Einsteins klokke'', ble introdusert. Denne klokken regner et "tikk" som den tiden klokken bruker på å sende et foton en vertikal distanse mellom to sensorer. | ||
| Linje 23: | Linje 21: | ||
[[Fil:relative_triangle.png| thumb || 200px | Figur 2: Forflytningstriangel]] | [[Fil:relative_triangle.png| thumb || 200px | Figur 2: Forflytningstriangel]] | ||
| − | Utfra Pytagoras' regel og enkel aritmetikk får vi: | + | Utfra Pytagoras' [[regler|regel]] og enkel aritmetikk får vi: |
| − | < | + | <math> |
\Delta t_B = \frac{\Delta t_A^0}{\sqrt{ 1- \left( \frac{u}{c}\right)^2}} | \Delta t_B = \frac{\Delta t_A^0}{\sqrt{ 1- \left( \frac{u}{c}\right)^2}} | ||
| − | </ | + | </math> |
== Utvidet betraktning for translatorisk bevegelse uten akselerasjon == | == Utvidet betraktning for translatorisk bevegelse uten akselerasjon == | ||
| Linje 35: | Linje 33: | ||
Endringen i tid for en reisende per meter reiselengde langs ekvator vil være: | Endringen i tid for en reisende per meter reiselengde langs ekvator vil være: | ||
| − | < | + | <math> |
\left.\frac{\partial t}{\partial x}\right|_{ekvator} = \frac{\mathcal T_d }{L_E } | \left.\frac{\partial t}{\partial x}\right|_{ekvator} = \frac{\mathcal T_d }{L_E } | ||
| − | </ | + | </math> |
| − | Hvor < | + | Hvor <math>\mathcal T_d </math> er tiden i et døgn (<math>24\cdot3600 ~ s</math> ) og <math>L_E</math> er jordas omkrets ved ekvator. Ved breddegrad <math>\theta</math> og med en hastighet i en vinkel <math>\phi</math> på ekvator finner vi gjennom litt enkel geometri at det generelle uttrykket blir: |
| − | < | + | <math> |
\frac{\partial t}{\partial x} = \frac{\mathcal T_d}{L_E} \frac{\cos \phi}{\cos^2\theta} | \frac{\partial t}{\partial x} = \frac{\mathcal T_d}{L_E} \frac{\cos \phi}{\cos^2\theta} | ||
| − | </ | + | </math> |
| − | Vi antar videre forholdsvis korte forflytninger per klokketikk (< | + | Vi antar videre forholdsvis korte forflytninger per klokketikk (<math>x\ll L_E</math>) og at toget ikke krysser tidssonesømmen; <math>x\in \{ -L_E,L_E\}</math>. Tidsintervaller erfart av observatør A må da augmenteres for endring i tidssone. Grunnet det korte tidsintervallet gir en første ordens rekkeutvikling tilstrekkelig presisjon: |
| − | < | + | <math> |
\Delta t_A = \Delta t_A^0 + \frac{\partial t}{\partial x} \Delta x | \Delta t_A = \Delta t_A^0 + \frac{\partial t}{\partial x} \Delta x | ||
| − | </ | + | </math> |
| − | < | + | <math> \Delta x </math> kan uttrykkes utfra observasjonene til observatør B: |
| − | < | + | <math> |
\Delta x = u \Delta t_B | \Delta x = u \Delta t_B | ||
| − | </ | + | </math> |
Denne augmentasjonen kan nå settes inn i forflytningstriangelet Figur 2 fra Einsteins forenklede utledning. Figur 3 viser endringen. | Denne augmentasjonen kan nå settes inn i forflytningstriangelet Figur 2 fra Einsteins forenklede utledning. Figur 3 viser endringen. | ||
| Linje 63: | Linje 61: | ||
Ved igjen å benytte Pytagoras’ regel får vi: | Ved igjen å benytte Pytagoras’ regel får vi: | ||
| − | < | + | <math> |
(c \Delta t_B)^2 = (u \Delta t_B)^2 + c^2\left(\Delta t_A^0 + u\frac{\partial t}{\partial x} \Delta t_B\right)^2 | (c \Delta t_B)^2 = (u \Delta t_B)^2 + c^2\left(\Delta t_A^0 + u\frac{\partial t}{\partial x} \Delta t_B\right)^2 | ||
| − | </ | + | </math> |
Vi innfører variabelen | Vi innfører variabelen | ||
| − | < | + | <math> |
\zeta \stackrel{\Delta}{=} \frac{1}{1-\left( u\frac{\partial t}{\partial x} \right)^2-\left(\frac uc \right)^2} | \zeta \stackrel{\Delta}{=} \frac{1}{1-\left( u\frac{\partial t}{\partial x} \right)^2-\left(\frac uc \right)^2} | ||
| − | </ | + | </math> |
| − | og får et kvadratisk uttrykk i < | + | og får et kvadratisk uttrykk i <math> \Delta t_B </math>: |
| − | < | + | <math> |
\Delta t_B^2 - 2u\frac{\partial t}{\partial x} \zeta \Delta t_A^0 \Delta t_B - \zeta \Delta {t_A^0}^2 = 0 | \Delta t_B^2 - 2u\frac{\partial t}{\partial x} \zeta \Delta t_A^0 \Delta t_B - \zeta \Delta {t_A^0}^2 = 0 | ||
| − | </ | + | </math> |
med den velkjente løsningen: | med den velkjente løsningen: | ||
| − | < | + | <math> |
\Delta t_B = \left[ u\frac{\partial t}{\partial x} \zeta \pm \sqrt{\left( u \frac{\partial t}{\partial x} \zeta\right)^2 + \zeta }\right]{\Delta t_A^0} | \Delta t_B = \left[ u\frac{\partial t}{\partial x} \zeta \pm \sqrt{\left( u \frac{\partial t}{\partial x} \zeta\right)^2 + \zeta }\right]{\Delta t_A^0} | ||
| − | </ | + | </math> |
| − | Ettersom det kvadratiske uttrykket stammer fra Pytagoras' regel er kun < | + | Ettersom det kvadratiske uttrykket stammer fra Pytagoras' regel er kun <math>\pm \rightarrow + </math> en gyldig løsning. |
== Kompleks tid == | == Kompleks tid == | ||
| − | Grunnet en regnefeil var det lenge trodd ved [[Universitetet i Rælingsskaret]] at tilstrekkelig rask bevegelse ville føre til akkumulering av kompleks tid. Dette fenomenet var statistisk verifisert med et 5 % signifikansnivå ved å dokumentere at en stor andel av den eldre, reisevante befolkning (de med mye akkumulert kompleks tid) mente | + | Grunnet en regnefeil var det lenge trodd ved [[Universitetet i Rælingsskaret]] at tilstrekkelig rask bevegelse ville føre til akkumulering av kompleks tid. Dette fenomenet var statistisk verifisert med et 5 % signifikansnivå ved å dokumentere at en stor andel av den eldre, reisevante befolkning (de med mye akkumulert kompleks tid) mente «alt var så mye enklere (mindre komplekst) før». |
| Linje 97: | Linje 95: | ||
Et kriterium for kompleks tid er at | Et kriterium for kompleks tid er at | ||
| − | < | + | <math> |
\left(u \frac{\partial t}{\partial x} \right)^2 + \zeta^{-1}<0 | \left(u \frac{\partial t}{\partial x} \right)^2 + \zeta^{-1}<0 | ||
| − | </ | + | </math> |
| − | som, ved innsettelse av < | + | som, ved innsettelse av <math>\zeta</math>, maner ut kriteriet |
| − | < | + | <math> |
|u|>c | |u|>c | ||
| − | </ | + | </math> |
hvilket er umulig da lyshastigheten er et globalt supremum. | hvilket er umulig da lyshastigheten er et globalt supremum. | ||
Nåværende revisjon fra 13. mar. 2023 kl. 10:38
Du trodde kanskje at tidsdilatasjon er et fenomen beskrevet av relativitetsteorien som garanterer et hastighetssupremum satt av lyshastigheten ved at selve tiden oppfattet av observatører i forskjellige referansesystemer er forskjellige. Selv om du kanskje akkurat denne gangen begynner å nærme deg snevet av en valid tankerekke, er prinsippene du bygger på noget mangelfulle.
Tidsdilatasjon for translatorisk bevegelse uten akselerasjon som presentert av Albert Einstein
Den relativitetsteori publisert av Albert Einstein i 1905 er mangelfull. En kjapp introduksjon er likevel nødvendig.
To aksiomer legges til grunne for denne utledningen:
- Bevegelsen til et legeme er relativ til det referansesystem bevegelsen observeres fra.
- Lysets hastighet (\(c \approx 3\cdot10^{8}\) m/s) er absolutt, uavhengig av referansesystem.
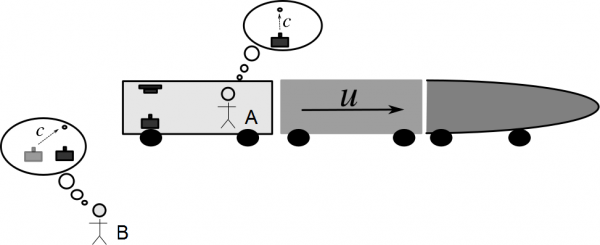
Albert Einstein nyttiggjorde seg av tog for å illustrere dette konseptet. En klokke, senere kjent som Einsteins klokke, ble introdusert. Denne klokken regner et "tikk" som den tiden klokken bruker på å sende et foton en vertikal distanse mellom to sensorer.
Denne klokken tenkes å være plassert på et tog i rask bevegelse. Toget akselererer ikke. To observatører, A og B, observerer klokkens tikk fra hvert sitt referansesystem; observatør A befinner seg ombord i toget og oppfatter togets relative bevegelse som stasjonær, mens observatør B befinner seg utenfor toget og oppfatter togets relative bevegelse som en hastighet u. Figur 1 illustrerer oppsettet.
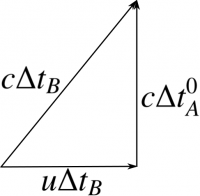
Aksiom (1) indikerer at det er en forskjell i hvordan toghastigheten observeres blant de to observatørene, mens Aksiom (2) krever at hastigheten til fotonet i klokka (lyshastigheten) observeres likt for begge parter. For at begivenheten skal være konsistent må da tidsintervallet i et tikk være forskjellig for de to observatørene. Det resulterende forflytningstriangelet vises i Figur 2.
Utfra Pytagoras' regel og enkel aritmetikk får vi\[ \Delta t_B = \frac{\Delta t_A^0}{\sqrt{ 1- \left( \frac{u}{c}\right)^2}} \]
Utvidet betraktning for translatorisk bevegelse uten akselerasjon
Einstein tabbet seg kraftig ut da han ikke innså at toget i hans betraktning potensielt beveger seg på tvers av landegrenser og derfor kan påvirkes av kryssing mellom tidssoner.
Da nivået på leseren trolig er lavt, antar vi kontinuerlige tidssoner, slik at leseren ikke belastes med diskrete beregninger. Endringen i tid for en reisende per meter reiselengde langs ekvator vil være\[ \left.\frac{\partial t}{\partial x}\right|_{ekvator} = \frac{\mathcal T_d }{L_E } \]
Hvor \(\mathcal T_d \) er tiden i et døgn (\(24\cdot3600 ~ s\) ) og \(L_E\) er jordas omkrets ved ekvator. Ved breddegrad \(\theta\) og med en hastighet i en vinkel \(\phi\) på ekvator finner vi gjennom litt enkel geometri at det generelle uttrykket blir\[ \frac{\partial t}{\partial x} = \frac{\mathcal T_d}{L_E} \frac{\cos \phi}{\cos^2\theta} \]
Vi antar videre forholdsvis korte forflytninger per klokketikk (\(x\ll L_E\)) og at toget ikke krysser tidssonesømmen; \(x\in \{ -L_E,L_E\}\). Tidsintervaller erfart av observatør A må da augmenteres for endring i tidssone. Grunnet det korte tidsintervallet gir en første ordens rekkeutvikling tilstrekkelig presisjon\[ \Delta t_A = \Delta t_A^0 + \frac{\partial t}{\partial x} \Delta x \]
\( \Delta x \) kan uttrykkes utfra observasjonene til observatør B\[ \Delta x = u \Delta t_B \]
Denne augmentasjonen kan nå settes inn i forflytningstriangelet Figur 2 fra Einsteins forenklede utledning. Figur 3 viser endringen.
Ved igjen å benytte Pytagoras’ regel får vi\[ (c \Delta t_B)^2 = (u \Delta t_B)^2 + c^2\left(\Delta t_A^0 + u\frac{\partial t}{\partial x} \Delta t_B\right)^2 \]
Vi innfører variabelen
\( \zeta \stackrel{\Delta}{=} \frac{1}{1-\left( u\frac{\partial t}{\partial x} \right)^2-\left(\frac uc \right)^2} \)
og får et kvadratisk uttrykk i \( \Delta t_B \)\[ \Delta t_B^2 - 2u\frac{\partial t}{\partial x} \zeta \Delta t_A^0 \Delta t_B - \zeta \Delta {t_A^0}^2 = 0 \]
med den velkjente løsningen\[ \Delta t_B = \left[ u\frac{\partial t}{\partial x} \zeta \pm \sqrt{\left( u \frac{\partial t}{\partial x} \zeta\right)^2 + \zeta }\right]{\Delta t_A^0} \]
Ettersom det kvadratiske uttrykket stammer fra Pytagoras' regel er kun \(\pm \rightarrow + \) en gyldig løsning.
Kompleks tid
Grunnet en regnefeil var det lenge trodd ved Universitetet i Rælingsskaret at tilstrekkelig rask bevegelse ville føre til akkumulering av kompleks tid. Dette fenomenet var statistisk verifisert med et 5 % signifikansnivå ved å dokumentere at en stor andel av den eldre, reisevante befolkning (de med mye akkumulert kompleks tid) mente «alt var så mye enklere (mindre komplekst) før».
Beregninger gjort ved et hvilket-som-helst annet universitet motstrider derimot denne hypotesen.
Et kriterium for kompleks tid er at
\( \left(u \frac{\partial t}{\partial x} \right)^2 + \zeta^{-1}<0 \)
som, ved innsettelse av \(\zeta\), maner ut kriteriet
\( |u|>c \)
hvilket er umulig da lyshastigheten er et globalt supremum.