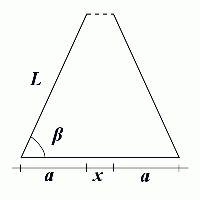Pikant
Du trodde kanskje at pikant var et adjektiv og betydde skarp eller pirrende? Det er fullstendig galt. En pikant er en geometrisk figur med π (pi) antall kanter.
Geometrisk tolkning
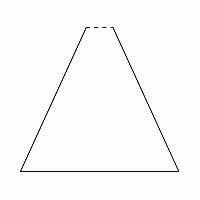
Geometrisk er en pikant en trekant som er litt åpnet, men ikke så mye at den har blitt en firkant.
Indre vinkel
Den indre vinkelen β, vinkelen i hørnet av en regulær mangekant, kan finnes slik:
<m> \beta=\pi\left(1-\frac{2}{n}\right) </m>
Innsatt for en pikant får vi
<m> \beta=\pi\left(1-\frac{2}{\pi}\right)=\pi-2\approx 1.14159\approx 65.4\textdegree </m>
Ytre vinkel
Den ytre vinkelen γ er tilsvarende for en regulær mangekant:
<m> \gamma=\pi\frac{2}{n} </m>
som for en pikant gir 2 radianer, eller 114,59 °.
Omkrets
Omkretsen av en generell n-kant med sidelengde L er nL. En pikant har omkrets πL.
Areal
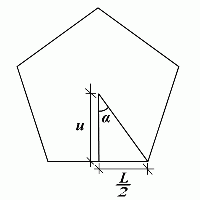
I en generell regulær mangekant med sidelengde L kan vi definere vinkelen α som vist på figuren. Vi definer så lengden u som avstanden fra figurens sentrum vinkelrett på midtpunktet til sidekanten.
Vikelen α er da halvparten av en full sirkel delt på n, eller målt i radianer:
<m> \alpha=\frac{1}{2}\frac{2\pi}{n}=\frac{\pi}{n} </m>
Lengden u defineres av forholdet:
<m> \mathrm{tan}\,\alpha=\frac{L/2}{u} </m>
Arealet av den fremkommende trekanten er:
<m> \frac{1}{2}u\frac{L}{2}=\frac{1}{4}uL </m>
Siden det er 2n slike trekanter i mangekanten er det totale arealet 2n ganger dette arealet.
Da er det totale arealet:
<m> A=2n\cdot\frac{1}{4}uL=2n\cdot\frac{1}{4}\frac{L/2}{\mathrm{tan}\,\alpha}L=n\frac{1}{4}\mathrm{cot}\,\alpha L^{2}=\frac{n}{4}\mathrm{cot}\,\frac{\pi}{n}L^{2} </m>
Arealet av en pikant får vi ved å sette n lik π:
<m> A=\frac{\pi}{4}\mathrm{cot}\,\frac{\pi}{\pi}L^{2}=\frac{\pi}{4}\mathrm{cot}\,1\cdot L^{2}\approx 0.504298 L^{2} </m>
Høyde
Høyden av en pikant gis av formelen
<m> h=L \mathrm{sin}\left(\beta\right)= L \mathrm{sin}\left(\pi - 2\right)\approx 0.9093 L </m>
Stjernepolygon
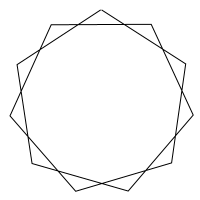
Den indre vinkelen er som nevnt over 65,4 °. Dette tilsvarer nesten perfekt en 5,5-deling av 360 grader, med et avvik på bare 0,070 %. Visuelt har derfor pikanten et nært forhold til en 11-kantet stjerne. Figuren under viser en pikantstjerne, et såkalt pikantagram. Ved å se nærmere på figuren kan du se at det er et tomrom mellom linjene i det øverste hjørnet.
Innskrevet og omskrevet sirkel
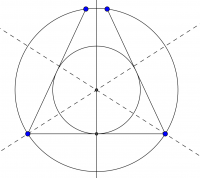
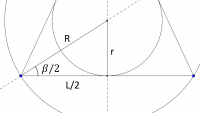
Senterpunktet for både innskrevet og omskrevet sirkel finnes i skjæringspunktet til linjene som halverer hjørnevinklene.
I figuren under er r og R radiene i henholdsvis den innskrevne og omskrevne sirkelen.
Innskrevet sirkel
Fra geometriske betraktninger i figuren over kan vi sette opp følgende formler:
<m> \mathrm{tan}\left(\beta\right)=\frac{r}{L/2}=\frac{2r}{L} </m>
Ved innsetting og omrokkering får vi:
<m> r=\frac{1}{2}\mathrm{tan}\left(\frac{\pi}{2}-1\right) L\approx 0.321 L </m>
Arealet av den innskrevne sirkelen blir da:
<m> A=\frac{\pi}{4}\mathrm{tan}^2\left(\frac{\pi}{2}-1\right)L^2\approx 0.324 L^2 </m>
som tilsvarer ca. 64 % av pikantens areal.
Omskrevet sirkel
Som for den innskrevne sirkelen kan vi sette opp et uttrykk for radien i den omskrevne sirkelen:
<m> \mathrm{cos}\left(\frac{\pi}{2}-1\right)=\frac{1/2}{R} L=\frac{L}{2R} </m>
<m> R=\frac{1}{2}\mathrm{sec}\left(\frac{\pi}{2}-1\right) L\approx 0.594 L </m>
Arealet av den omskrevne sirkelen blir da:
<m> A=\frac{\pi}{4}\mathrm{sec}^2\left(\frac{\pi}{2}-1\right) L^2 \approx 1.109 L^2 </m>
som tilsvarer ca. 220 % av pikantens areal.
Den åpne siden
Det er vitenskapelige stridigheter om tolkningen av den åpne siden av pikanten. Man vet at den har lengden (π - 3) L ≈ 0.1416 L, men dette strider med at det er en rett linje, siden avstanden mellom de to endepunktene i euklidsk geometri er ≈ 0.1677 L, som vist i det følgende:
<m> \beta=\pi-2 </m>
<m> \mathrm{cos}\,\beta=\frac{a}{L}\Rightarrow a=L\,\mathrm{cos}\,\beta </m>
<m> x=L-2a=L-2L\,\mathrm{cos}\,\beta=L\left(1-2\,\mathrm{cos}\,\beta\right)=L\left(1-2\,\mathrm{cos}\,\left(\pi-2\right)\right)\approx 0.1677 L </m>
- Enkelte matematikere mener at en pikant egentlig er en tredimensjonal figur som er projisert inn i xy-planet.
- Andre hevder at de ekstra 0.0026 L kommer fra luftforurensning i Asia.
- Den åpne siden er også blitt brukt til narkotikasmugling.
Tyngdepunkt
Tyngdepunktet kan beregnes etter følgende måte:
<m> c_y=\frac{x \cdot h \cdot \frac{h}{2} + a \cdot h \cdot \frac{h}{3}}{x \cdot h + a \cdot h} </m>
Dette kan forenkles til
<m> \frac{h}{6} \frac{3 x + 2 a}{x + a} </m>
Ved innsetting får man
<m> c_y\approx 0.3466 L </m>
Anvendelse
Den viktigste anvendelsen av den geometriske formen til en pikant er ved produksjon av musikkinstrumentet triangel. Vinkelens forhold til π og sirkelen gir instrumentet en spesielt rund lyd.