Forskjell mellom versjoner av «Alkohol»
| (10 mellomliggende revisjoner av samme bruker vises ikke) | |||
| Linje 1: | Linje 1: | ||
| − | <onlyinclude>Du trodde kanskje at du drakk for å glemme? Da har du nok glemt at du allerede er full. Hvis du benytter '''alkohol''' fordi du er i ferd med å gå inn i en depresjon vil nemlig depresjonen bare bli dypere.</onlyinclude> | + | <onlyinclude><includeonly>thumb|Rustransformert.png</includeonly>Du trodde kanskje at du drakk for å glemme? Da har du nok glemt at du allerede er full. Hvis du benytter '''alkohol''' fordi du er i ferd med å gå inn i en depresjon vil nemlig depresjonen bare bli dypere.</onlyinclude> |
== Bakgrunn == | == Bakgrunn == | ||
| − | Hvis du drikker på stigende humør, vil du få en positiv rus, men hvis du drikker på synkende humør, vil rusen være negativ. Hvis du i utgangspunktet har et konstant humør når du drikker, vil | + | Hvis du drikker på stigende humør, vil du få en positiv rus, men hvis du drikker på synkende humør, vil rusen være negativ. Hvis du i utgangspunktet har et konstant humør når du drikker, vil humøret bli helt flatt. |
Når du er beruset er det ikke ditt virkelige humør som kommer til overflaten, men den rustransformerte humørfunksjonen. Hele tiden mens du er beruset har du et underliggende humør som først kan sees direkte igjen når promillen din blir null. | Når du er beruset er det ikke ditt virkelige humør som kommer til overflaten, men den rustransformerte humørfunksjonen. Hele tiden mens du er beruset har du et underliggende humør som først kan sees direkte igjen når promillen din blir null. | ||
== Matematisk grunnlag == | == Matematisk grunnlag == | ||
| − | Humøret ditt kan defineres med en dimensjonsløs parameter < | + | Humøret ditt kan defineres med en dimensjonsløs parameter <math>\psi</math> på den reelle tallinjen. <math>\psi=0</math> tilsvarer et nøytralt humør, og positive verdier tilsvarer et godt humør. Ved beruselse vil det rustransformerte humøret <math>\zeta</math> komme til overflaten. <math>\zeta</math> kan beregnes ved å derivere humørfunksjonen med hensyn på tiden, som vist i utledningen under. |
== Fraksjonal derivasjon == | == Fraksjonal derivasjon == | ||
| − | Stigningstallet til en funksjon < | + | Stigningstallet til en funksjon <math>f\left(x\right)</math> finnes ved den deriverte, <math>f'\left(x\right)</math> eller <math>\frac{d}{dx}f\left(x\right)</math>. For en [[potensfunksjon]], eller et enkelt ledd i en polynomfunksjon, <math>f\left(x\right)=ax^{b}</math>, kan den deriverte finnes som <math>f'\left(x\right)=bax^{b-1}</math>. Den andrederiverte finnes ved å derivere den deriverte:<math>f''\left(x\right)=b\left(b-1\right)ax^{b-2}</math>, og den tredjederiverte som <math>f'''\left(x\right)=b\left(b-1\right)\left(b-2\right)ax^{b-3}</math>. |
| − | Ved å fortsette rekken kan det vises at den n-te-deriverte kan skrives som < | + | Ved å fortsette rekken kan det vises at den n-te-deriverte kan skrives som <math>f^{\left(n\right)}\left(x\right)=\frac{b!}{\left(b-n\right)!}ax^{b-n}</math>. |
| − | Vi kan erstatte fakultetfunksjonen med gammafunksjonen ved å benytte at < | + | Vi kan erstatte fakultetfunksjonen med gammafunksjonen ved å benytte at <math>x!=\Gamma\left(x+1\right)</math>. Vi får da det generelle uttrykket for den n-te-deriverte <math>f^{\left(n\right)}\left(x\right)=\frac{b!}{\Gamma\left(b-n+1\right)}ax^{b-n}</math>, der ''n'' ikke nødvendigvis er et heltall. Dette betegnes fraksjonalderivasjon, men det er du for full til å forstå. |
| − | En vilkårlig funksjon ''f''(''x'') som er uendelig differensierbar på ''x''=''h'' kan skrives som en polynomfunksjon ved Taylor-rekkeutvikling:< | + | En vilkårlig funksjon ''f''(''x'') som er uendelig differensierbar på ''x''=''h'' kan skrives som en polynomfunksjon ved Taylor-rekkeutvikling:<math>f(x)=\sum_{i=0}^{\infty} \frac{f^{\left(i\right)}\left(h\right)}{i!} \left(x-h\right)^i.</math> |
Ved rekkeutvikling rundt ''x''=0 kan dette skrives som | Ved rekkeutvikling rundt ''x''=0 kan dette skrives som | ||
| − | < | + | <math>f(x)=\sum_{i=0}^{\infty}a_{i}x^{i}</math> der <math>a_i=\frac{f^{\left(i\right)}\left(h\right)}{i!}</math>, |
og vi kan slik uttrykke den generelle fraksjonalderiverte av en vilkårlig funksjon med uttrykket | og vi kan slik uttrykke den generelle fraksjonalderiverte av en vilkårlig funksjon med uttrykket | ||
| − | < | + | <math> |
f^{\left(n\right)}(x)=\sum_{i=0}^{\infty} \frac{i!}{\Gamma\left(i-n+1\right)}a_{i}x^{i-n} | f^{\left(n\right)}(x)=\sum_{i=0}^{\infty} \frac{i!}{\Gamma\left(i-n+1\right)}a_{i}x^{i-n} | ||
| − | </ | + | </math>. |
== Rustransformasjon == | == Rustransformasjon == | ||
| − | Graden av beruselse bestemmer hvor mye humørfunksjonen skal fraksjonalderiveres. Vi kan definere beruselsesgraden med parameteren < | + | Graden av beruselse bestemmer hvor mye humørfunksjonen skal fraksjonalderiveres. Vi kan definere beruselsesgraden med parameteren <math>\rho=\frac{p}{p_0}</math>, der ''p'' er alkoholpromillen og ''p<sub>0</sub>'' er den individuelle grenseverdien for promille, som avhenger av alkoholtoleranse. For en gjennomsnittlig person ligger ''p<sub>0</sub>'' et sted i intervallet 2-5 ‰, men for personer med alkoholisme som hovedlevevei kan ''p<sub>0</sub>'' være så høy som 10 eller 15 ‰. |
Uttrykket for den rustransformerte humørfunksjonen er derfor | Uttrykket for den rustransformerte humørfunksjonen er derfor | ||
| − | < | + | <math> |
| − | \zeta=\psi^{\left(\rho\right)}(t)=\sum_{i=0}^{\infty} \frac{ | + | \zeta=\psi^{\left(\rho\right)}(t)=\sum_{i=0}^{\infty} \frac{i!}{\Gamma\left(i-\rho+1\right)}a_{i}t^{i-\rho} |
| − | </ | + | </math>. |
| + | |||
| + | == Alternativ modell == | ||
| + | |||
| + | Siden du trolig ikke klarer å holde orden på den avanserte matematikken over, presenteres også en litt lettere modell. | ||
| + | |||
| + | Modellen forutsetter at ved fullstendig beruselse, ''ρ'' = 1.0, er den rustransformerte humørfunksjonen lik en konstant ''k'' multiplisert med den deriverte av humørfunksjonen. Et stigende faktisk humør gir altså positivt rustransformert humør. Ved ''ρ'' = 0 er naturlig nok den rustransformerte humørfunksjonen lik det faktiske humøret. Ved 0 < ''ρ'' < 1 benyttes lineær interpolasjon mellom de to verdiene. | ||
| + | |||
| + | I eksempelet under er skaleringen ''k'' satt til 3, og promilleterskelen er satt til 2. Den underliggende humørfunksjonen følger en tredjegradsfunksjon med synkende humør i begynnelsen og mot slutten, og stigende humør i midten av perioden. Alkoholpromillen følger kurven i den øverste figuren, og når nesten opp til promilleterskelen på det meste. | ||
| + | |||
| + | [[Image:Rustransformert.png|alt=Faktisk og rustransformert humørforløp gjennom en fyllekule|Faktisk og rustransformert humørforløp gjennom en fyllekule]] | ||
| + | |||
| + | Den gule linjen viser den fullt transformerte humørfunksjonen, altså slik humøret ville ha vært ved ''ρ'' = 1.0. Den rustransformerte humørfunksjonen ligger mellom den faktiske og den fullt transformerte funksjonen, og nærmer seg den fullt transformerte der promillen går mot terskelverdien. | ||
| + | |||
| + | Selv om det underliggende humøret i hovedsak er negativt, ligger den rustransformerte humørfunksjonen på positiv side der humørfunksjonen er stigende og promilleverdien er tilstrekkelig høy. | ||
| + | |||
| + | == Konklusjon == | ||
| + | |||
| + | For å utnytte effekten av rustransformasjon, bør man sørge for at den rustransformerte aldri ligger lavere enn humørfunksjonen, som vist i eksempelet over. | ||
| + | |||
| + | Dette gjør man best ved å sørge for en høyest promille når den underliggende humørfunksjonen er negativ, men stigende, for eksempel på vei ut av en lettere depresjon. Når humørfunksjonen er positiv, er det sjelden mye å hente på å øke promillen, og det innebærer en fare for at humørfunksjonen begynner å synke mens alkoholpromillen er høy, slik at den rustransformerte blir negativ. | ||
| + | |||
| + | Det problematiske er å vite hvordan den underliggende humørfunksjonen utvikler seg mens promillen er høy, slik at man kan planlegge videre alkoholkonsum. | ||
[[Kategori:Matematikk]] | [[Kategori:Matematikk]] | ||
[[Kategori:Rus]] | [[Kategori:Rus]] | ||
Nåværende revisjon fra 13. mar. 2023 kl. 11:45
Du trodde kanskje at du drakk for å glemme? Da har du nok glemt at du allerede er full. Hvis du benytter alkohol fordi du er i ferd med å gå inn i en depresjon vil nemlig depresjonen bare bli dypere.
Bakgrunn
Hvis du drikker på stigende humør, vil du få en positiv rus, men hvis du drikker på synkende humør, vil rusen være negativ. Hvis du i utgangspunktet har et konstant humør når du drikker, vil humøret bli helt flatt.
Når du er beruset er det ikke ditt virkelige humør som kommer til overflaten, men den rustransformerte humørfunksjonen. Hele tiden mens du er beruset har du et underliggende humør som først kan sees direkte igjen når promillen din blir null.
Matematisk grunnlag
Humøret ditt kan defineres med en dimensjonsløs parameter \(\psi\) på den reelle tallinjen. \(\psi=0\) tilsvarer et nøytralt humør, og positive verdier tilsvarer et godt humør. Ved beruselse vil det rustransformerte humøret \(\zeta\) komme til overflaten. \(\zeta\) kan beregnes ved å derivere humørfunksjonen med hensyn på tiden, som vist i utledningen under.
Fraksjonal derivasjon
Stigningstallet til en funksjon \(f\left(x\right)\) finnes ved den deriverte, \(f'\left(x\right)\) eller \(\frac{d}{dx}f\left(x\right)\). For en potensfunksjon, eller et enkelt ledd i en polynomfunksjon, \(f\left(x\right)=ax^{b}\), kan den deriverte finnes som \(f'\left(x\right)=bax^{b-1}\). Den andrederiverte finnes ved å derivere den deriverte\[f''\left(x\right)=b\left(b-1\right)ax^{b-2}\], og den tredjederiverte som \(f'''\left(x\right)=b\left(b-1\right)\left(b-2\right)ax^{b-3}\).
Ved å fortsette rekken kan det vises at den n-te-deriverte kan skrives som \(f^{\left(n\right)}\left(x\right)=\frac{b!}{\left(b-n\right)!}ax^{b-n}\).
Vi kan erstatte fakultetfunksjonen med gammafunksjonen ved å benytte at \(x!=\Gamma\left(x+1\right)\). Vi får da det generelle uttrykket for den n-te-deriverte \(f^{\left(n\right)}\left(x\right)=\frac{b!}{\Gamma\left(b-n+1\right)}ax^{b-n}\), der n ikke nødvendigvis er et heltall. Dette betegnes fraksjonalderivasjon, men det er du for full til å forstå.
En vilkårlig funksjon f(x) som er uendelig differensierbar på x=h kan skrives som en polynomfunksjon ved Taylor-rekkeutvikling\[f(x)=\sum_{i=0}^{\infty} \frac{f^{\left(i\right)}\left(h\right)}{i!} \left(x-h\right)^i.\] Ved rekkeutvikling rundt x=0 kan dette skrives som \(f(x)=\sum_{i=0}^{\infty}a_{i}x^{i}\) der \(a_i=\frac{f^{\left(i\right)}\left(h\right)}{i!}\), og vi kan slik uttrykke den generelle fraksjonalderiverte av en vilkårlig funksjon med uttrykket
\( f^{\left(n\right)}(x)=\sum_{i=0}^{\infty} \frac{i!}{\Gamma\left(i-n+1\right)}a_{i}x^{i-n} \).
Rustransformasjon
Graden av beruselse bestemmer hvor mye humørfunksjonen skal fraksjonalderiveres. Vi kan definere beruselsesgraden med parameteren \(\rho=\frac{p}{p_0}\), der p er alkoholpromillen og p0 er den individuelle grenseverdien for promille, som avhenger av alkoholtoleranse. For en gjennomsnittlig person ligger p0 et sted i intervallet 2-5 ‰, men for personer med alkoholisme som hovedlevevei kan p0 være så høy som 10 eller 15 ‰.
Uttrykket for den rustransformerte humørfunksjonen er derfor
\( \zeta=\psi^{\left(\rho\right)}(t)=\sum_{i=0}^{\infty} \frac{i!}{\Gamma\left(i-\rho+1\right)}a_{i}t^{i-\rho} \).
Alternativ modell
Siden du trolig ikke klarer å holde orden på den avanserte matematikken over, presenteres også en litt lettere modell.
Modellen forutsetter at ved fullstendig beruselse, ρ = 1.0, er den rustransformerte humørfunksjonen lik en konstant k multiplisert med den deriverte av humørfunksjonen. Et stigende faktisk humør gir altså positivt rustransformert humør. Ved ρ = 0 er naturlig nok den rustransformerte humørfunksjonen lik det faktiske humøret. Ved 0 < ρ < 1 benyttes lineær interpolasjon mellom de to verdiene.
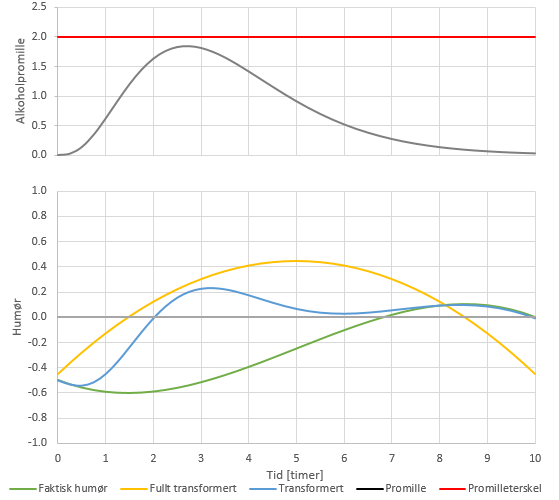
I eksempelet under er skaleringen k satt til 3, og promilleterskelen er satt til 2. Den underliggende humørfunksjonen følger en tredjegradsfunksjon med synkende humør i begynnelsen og mot slutten, og stigende humør i midten av perioden. Alkoholpromillen følger kurven i den øverste figuren, og når nesten opp til promilleterskelen på det meste.
Den gule linjen viser den fullt transformerte humørfunksjonen, altså slik humøret ville ha vært ved ρ = 1.0. Den rustransformerte humørfunksjonen ligger mellom den faktiske og den fullt transformerte funksjonen, og nærmer seg den fullt transformerte der promillen går mot terskelverdien.
Selv om det underliggende humøret i hovedsak er negativt, ligger den rustransformerte humørfunksjonen på positiv side der humørfunksjonen er stigende og promilleverdien er tilstrekkelig høy.
Konklusjon
For å utnytte effekten av rustransformasjon, bør man sørge for at den rustransformerte aldri ligger lavere enn humørfunksjonen, som vist i eksempelet over.
Dette gjør man best ved å sørge for en høyest promille når den underliggende humørfunksjonen er negativ, men stigende, for eksempel på vei ut av en lettere depresjon. Når humørfunksjonen er positiv, er det sjelden mye å hente på å øke promillen, og det innebærer en fare for at humørfunksjonen begynner å synke mens alkoholpromillen er høy, slik at den rustransformerte blir negativ.
Det problematiske er å vite hvordan den underliggende humørfunksjonen utvikler seg mens promillen er høy, slik at man kan planlegge videre alkoholkonsum.