Forskjell mellom versjoner av «Søvn»
| (Én mellomliggende revisjon av samme bruker vises ikke) | |||
| Linje 19: | Linje 19: | ||
Dersom du sov lite forrige natt, vil du behøve mer søvn neste natt, men ikke nødvendigvis hele mellomlegget. Søvnkonserveringsfaktoren ''α'' forteller hvor stor andel av søvnunderskuddet som vedvarer etter 24 timer. ''α'' = 0,25 sier for eksempel at et underskudd på to timer søvn en natt gjør at du må sove 0,25 * 2 = 0,5 timer lenger enn normalt natten etter. Verdien av søvnkonserveringsfaktoren varierer mye i litteraturen, fra 0,001 til 0,8. Mange forenklede søvnmodeller legger enten α = 0 eller α = 1 til grunn, altså enten at det ikke finnes lagring av søvnunderskudd eller at alt underskuddet overføres til neste natt. Metametastudier ved [[Universitetet i Rælingsskaret]] antyder at en verdi mellom 0,1 og 0,6 vil kunne forsvares fysisk. | Dersom du sov lite forrige natt, vil du behøve mer søvn neste natt, men ikke nødvendigvis hele mellomlegget. Søvnkonserveringsfaktoren ''α'' forteller hvor stor andel av søvnunderskuddet som vedvarer etter 24 timer. ''α'' = 0,25 sier for eksempel at et underskudd på to timer søvn en natt gjør at du må sove 0,25 * 2 = 0,5 timer lenger enn normalt natten etter. Verdien av søvnkonserveringsfaktoren varierer mye i litteraturen, fra 0,001 til 0,8. Mange forenklede søvnmodeller legger enten α = 0 eller α = 1 til grunn, altså enten at det ikke finnes lagring av søvnunderskudd eller at alt underskuddet overføres til neste natt. Metametastudier ved [[Universitetet i Rælingsskaret]] antyder at en verdi mellom 0,1 og 0,6 vil kunne forsvares fysisk. | ||
| − | Underskudd og overskudd av søvn kan bygge seg opp over tid, og konserveringsfaktoren forteller noe om hvor fort opparbeidet ubalanse brytes ned, eller eventuelt hvor langsomt det bygger seg opp. Et underskudd på ''x'' timer hver natt i en lengre periode vil over tid bygge seg opp til < | + | Underskudd og overskudd av søvn kan bygge seg opp over tid, og konserveringsfaktoren forteller noe om hvor fort opparbeidet ubalanse brytes ned, eller eventuelt hvor langsomt det bygger seg opp. Et underskudd på ''x'' timer hver natt i en lengre periode vil over tid bygge seg opp til <math>\frac{\alpha}{1-\alpha}x</math> timer. |
Søvnkonservering gjør at linjene i diagrammet ikke blir rette, men kurvede, som vist i figuren under. | Søvnkonservering gjør at linjene i diagrammet ikke blir rette, men kurvede, som vist i figuren under. | ||
| Linje 31: | Linje 31: | ||
Vi kan skrive at: | Vi kan skrive at: | ||
| − | d | + | <math>\frac{d\phi}{dt} = -a_0 k\phi \text{ for } i=0</math> |
| − | + | ||
| + | <math>\frac{d\phi}{dt} = a_1 k\phi \text{ for } i=1</math> | ||
Dette tilsvarer funksjonen | Dette tilsvarer funksjonen | ||
| − | + | <math>\phi = c_0 e^{-kt} - a_0 k \text{ for } i=0</math> | |
| − | + | ||
| + | <math>\phi = c_1 e^{-kt} + a_1 k \text{ for } i=1</math> | ||
der ''t'' er tiden i døgn ''c<sub>0</sub>'' og ''c<sub>1</sub>'' er integrasjonskonstanter. | der ''t'' er tiden i døgn ''c<sub>0</sub>'' og ''c<sub>1</sub>'' er integrasjonskonstanter. | ||
| Linje 43: | Linje 45: | ||
For gitte verdier av ''S'' og ''α'' kan vi beregne akkumulasjonskonstantene ''a</sub>0</sub>'' og ''a</sub>1</sub>'': | For gitte verdier av ''S'' og ''α'' kan vi beregne akkumulasjonskonstantene ''a</sub>0</sub>'' og ''a</sub>1</sub>'': | ||
| − | + | <math>a_0 = \frac{k}{e^{1-s/24} - 1}</math>, <math>a_1 = \frac{k}{1-e^{1-s/24}}</math> | |
== Praktisk anvendelse == | == Praktisk anvendelse == | ||
| − | Søvnmodellen er ikke bare en teoretisk modell, men ment for praktisk bruk. Spesielt nyttig er modellen for å planlegge leggetid og tid for å stå opp ved diskontinuiteter i den statiske døgnrytmen | + | Søvnmodellen er ikke bare en teoretisk modell, men ment for praktisk bruk. Spesielt nyttig er modellen for å planlegge leggetid og tid for å stå opp ved diskontinuiteter i den statiske døgnrytmen. |
=== Dagen etter fest === | === Dagen etter fest === | ||
En person med søvnbehov ''S''=8 timer står opp uthvilt lørdag kl. 8. Lørdag kveld er det fest, og personen legger seg ikke før kl. 4. For å få en behagelig søndag, sover personen helt ut søndag morgen, og tenker å legge seg igjen på et passende tidspunkt for å våkne til jobb kl. 6 mandag morgen. Se figur ''a'' til høyre. | En person med søvnbehov ''S''=8 timer står opp uthvilt lørdag kl. 8. Lørdag kveld er det fest, og personen legger seg ikke før kl. 4. For å få en behagelig søndag, sover personen helt ut søndag morgen, og tenker å legge seg igjen på et passende tidspunkt for å våkne til jobb kl. 6 mandag morgen. Se figur ''a'' til høyre. | ||
| − | I realiteten er dette vanskelig, siden man ikke rekker å bli tilstrekkelig trett søndag kveld. Resultatet blir at personen ligger våken i senga til kl. | + | I realiteten er dette vanskelig, siden man ikke rekker å bli tilstrekkelig trett søndag kveld. Resultatet blir at personen ligger våken i senga til kl. kvart på fem, og dermed ikke er uthvilt til jobb mandag morgen. Se figur ''b'' til høyre. |
Løsningen på problemet er å tilpasse oppvåkningen søndag morgen. Vi må finne oppvåkningstidspunktet som gjør at man blir trett igjen til ønsket tidspunkt. Se figur ''c'' til høyre. | Løsningen på problemet er å tilpasse oppvåkningen søndag morgen. Vi må finne oppvåkningstidspunktet som gjør at man blir trett igjen til ønsket tidspunkt. Se figur ''c'' til høyre. | ||
| − | Matematisk kan vi løse dette ved å sette de to uttrykkene for tretthet lik hverandre med grensebetingelsene i hver ende. I uttrykket under er | + | Matematisk kan vi løse dette ved å sette de to uttrykkene for tretthet lik hverandre med grensebetingelsene i hver ende. I uttrykket under er u<sub>1</sub> sovetid og Δ''t''=''u''<sub>1</sub>+''v''<sub>1</sub> tiden mellom leggetid lørdag og leggetid søndag, med døgn som enhet. φ<sub>0</sub> er trettheten ved leggetid lørdag. |
[[File:SøvnHelgA.png|400px|Plan|a]] | [[File:SøvnHelgA.png|400px|Plan|a]] | ||
| Linje 70: | Linje 72: | ||
[[File:SøvnJetVest.png|400px|Jetlag vest]] | [[File:SøvnJetVest.png|400px|Jetlag vest]] | ||
| − | Hvis vi kaller tiden fra man står opp den første og andre dagen for og Δt= | + | Hvis vi kaller tiden fra man står opp den første og andre dagen for og Δt=v<sub>0</sub>+u<sub>1</sub>, kan våkentiden v<sub>0</sub> regnes ut slik: |
Med søvnbehov ''S''=7 timer, søvnkonserveringsfaktor ''α''=0.3 og tidsforskjell -6 timer skal man være våken 22 timer og 2 minutter den første natten for å bli uthvilt til rett tid neste morgen. | Med søvnbehov ''S''=7 timer, søvnkonserveringsfaktor ''α''=0.3 og tidsforskjell -6 timer skal man være våken 22 timer og 2 minutter den første natten for å bli uthvilt til rett tid neste morgen. | ||
| Linje 76: | Linje 78: | ||
=== Jetlag øst === | === Jetlag øst === | ||
| − | Ved reise mot øst viser klokken plutselig et mye senere tidspunkt enn kroppen er forberedt på. Det er ikke lett å sovne til lokal tid første natten, så man bør være oppe til vanlig leggetid hjemme og deretter tilpasse tidspunktet man står opp slik at man blir trett til riktig tid neste natt. Dette tilsvarer situasjonen med dagen etter en fest over, med | + | Ved reise mot øst viser klokken plutselig et mye senere tidspunkt enn kroppen er forberedt på. Det er ikke lett å sovne til lokal tid første natten, så man bør være oppe til vanlig leggetid hjemme og deretter tilpasse tidspunktet man står opp slik at man blir trett til riktig tid neste natt. Dette tilsvarer situasjonen med dagen etter en fest over, med φ<sub>0</sub> = 1. |
| − | Hvis vi kaller tiden fra man legger seg den første og andre natten for Δt= | + | Hvis vi kaller tiden fra man legger seg den første og andre natten for Δt=u<sub>1</sub>+v<sub>1</sub>, kan sovetiden u<sub>1</sub> regnes ut slik: |
Med søvnbehov S=7 timer, søvnkonserveringsfaktor α=0.3 og tidsforskjell +6 timer skal man sove 4 timer og 40 minutter den første natten for å bli trett til riktig tid neste kveld. | Med søvnbehov S=7 timer, søvnkonserveringsfaktor α=0.3 og tidsforskjell +6 timer skal man sove 4 timer og 40 minutter den første natten for å bli trett til riktig tid neste kveld. | ||
Nåværende revisjon fra 17. jun. 2024 kl. 11:37
Du trodde kanskje at kroppen selv er den beste til å bedømme hvor mye søvn du trenger? I så fall trenger du en real oppvåkning: Riktig mengde søvn kan bare finnes ved bruk av matematikk.
Søvnbehov
Søvnbehovet per natt, S, varierer mye fra person til person, normalt i intervallet 5-10 timer. Dette er avhengig av kulturelle og individuelle faktorer, og vil påvirkes av livsstil.
Tretthet
Tretthet er kroppens måte å si ifra at det er på tide å sove. Ved stabil døgnrytme vil man bli trett og merke at man er klar for å sove når man har vært våken i 24 - S timer. Ved et søvnbehov på 6 timer blir man for eksempel trett etter 24 - 6 = 18 timer.
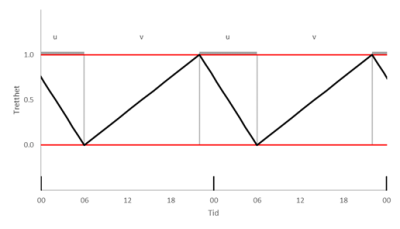
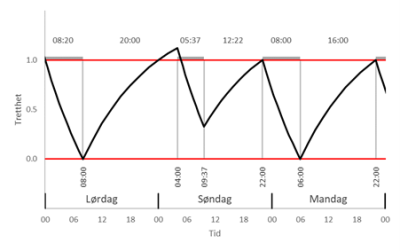
En søvnsyklus består av to faser: søvnfase og våkenfase. Ved statisk to-fase døgnrytme vil lengden av søvnfasen være u=S, og lengden av våkenfasen vil være v=24t-S. En vanlig søvnrytme kan tenkes å se slik ut:
Figuren viser en periode på to døgn, med klokkeslettet nederst. De grå feltene markerer søvnfasene. Vi ser at trettheten øker fra våknenivået om morgenen til sovnenivået om kvelden, før den synker til våknenivået igjen neste morgen.
Normalt er det vanskelig å sove lenger enn til uthvilt tilstand, slik at det er sjelden man kommer langt under den nedre grenseverdien i diagrammet. Samtidig er det vanskelig å falle i søvn før man er helt trett, slik at toppene i diagrammet som oftest vil stikke minst opp til den øvre grenseverdien.
Konservering av søvn
Dersom du sov lite forrige natt, vil du behøve mer søvn neste natt, men ikke nødvendigvis hele mellomlegget. Søvnkonserveringsfaktoren α forteller hvor stor andel av søvnunderskuddet som vedvarer etter 24 timer. α = 0,25 sier for eksempel at et underskudd på to timer søvn en natt gjør at du må sove 0,25 * 2 = 0,5 timer lenger enn normalt natten etter. Verdien av søvnkonserveringsfaktoren varierer mye i litteraturen, fra 0,001 til 0,8. Mange forenklede søvnmodeller legger enten α = 0 eller α = 1 til grunn, altså enten at det ikke finnes lagring av søvnunderskudd eller at alt underskuddet overføres til neste natt. Metametastudier ved Universitetet i Rælingsskaret antyder at en verdi mellom 0,1 og 0,6 vil kunne forsvares fysisk.
Underskudd og overskudd av søvn kan bygge seg opp over tid, og konserveringsfaktoren forteller noe om hvor fort opparbeidet ubalanse brytes ned, eller eventuelt hvor langsomt det bygger seg opp. Et underskudd på x timer hver natt i en lengre periode vil over tid bygge seg opp til \(\frac{\alpha}{1-\alpha}x\) timer.
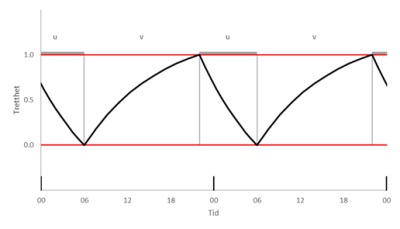
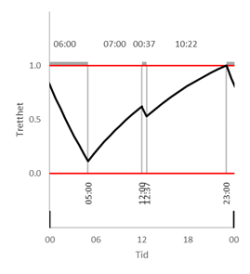
Søvnkonservering gjør at linjene i diagrammet ikke blir rette, men kurvede, som vist i figuren under.
Matematisk modell
Vi måler trettheten φ på en dimensjonsløs skala der 0 og 1 tilsvarer henholdsvis sovne- og våkne-nivået. Tretthetsmodellen har to ledd: akkumulasjon og dissipasjon. Akkumulasjon er den lineære økningen eller reduksjonen i tretthet som følge av sovende eller våken tilstand. Trettheten øker eller synker med en konstant verdi ai per tidsenhet, der tilstanden i er 0 for sovende og 1 for våken tilstand. Denne konstanten er forskjellig for sovende og våken tilstand. Samtidig dissiperer trettheten med en dissipasjonsrate som er proporsjonal med trettheten, Vi kaller dissipasjonskoeffisienten k. Vi kan skrive at\[\frac{d\phi}{dt} = -a_0 k\phi \text{ for } i=0\]
\(\frac{d\phi}{dt} = a_1 k\phi \text{ for } i=1\)
Dette tilsvarer funksjonen
\(\phi = c_0 e^{-kt} - a_0 k \text{ for } i=0\)
\(\phi = c_1 e^{-kt} + a_1 k \text{ for } i=1\)
der t er tiden i døgn c0 og c1 er integrasjonskonstanter. Proporsjonalitetskonstanten beregnes som k=-ln α. For gitte verdier av S og α kan vi beregne akkumulasjonskonstantene a0 og a1\[a_0 = \frac{k}{e^{1-s/24} - 1}\], \(a_1 = \frac{k}{1-e^{1-s/24}}\)
Praktisk anvendelse
Søvnmodellen er ikke bare en teoretisk modell, men ment for praktisk bruk. Spesielt nyttig er modellen for å planlegge leggetid og tid for å stå opp ved diskontinuiteter i den statiske døgnrytmen.
Dagen etter fest
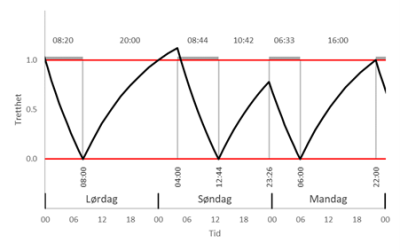
En person med søvnbehov S=8 timer står opp uthvilt lørdag kl. 8. Lørdag kveld er det fest, og personen legger seg ikke før kl. 4. For å få en behagelig søndag, sover personen helt ut søndag morgen, og tenker å legge seg igjen på et passende tidspunkt for å våkne til jobb kl. 6 mandag morgen. Se figur a til høyre.
I realiteten er dette vanskelig, siden man ikke rekker å bli tilstrekkelig trett søndag kveld. Resultatet blir at personen ligger våken i senga til kl. kvart på fem, og dermed ikke er uthvilt til jobb mandag morgen. Se figur b til høyre.
Løsningen på problemet er å tilpasse oppvåkningen søndag morgen. Vi må finne oppvåkningstidspunktet som gjør at man blir trett igjen til ønsket tidspunkt. Se figur c til høyre. Matematisk kan vi løse dette ved å sette de to uttrykkene for tretthet lik hverandre med grensebetingelsene i hver ende. I uttrykket under er u1 sovetid og Δt=u1+v1 tiden mellom leggetid lørdag og leggetid søndag, med døgn som enhet. φ0 er trettheten ved leggetid lørdag.
I det gitte eksempelet, og med α = 0.2, bør personen sove 5 timer og 37 minutter for å bli trett til riktig tid på søndag.
Jetlag vest
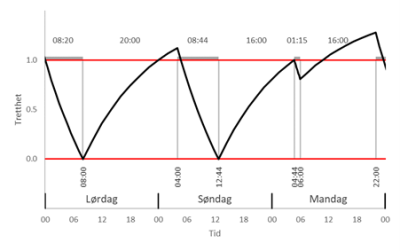
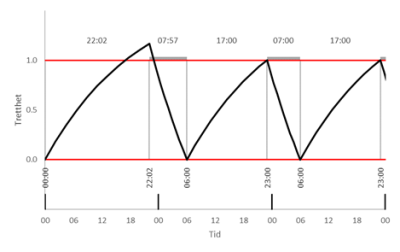
Ved reise mot vest viser klokken plutselig et mye tidligere tidspunkt enn kroppen er forberedt på. Hvis man legger seg når man blir trett, vil dagene fortsette å være forskjøvet. Man bør derfor holde ut litt til den første kvelden, slik at man blir uthvilt til riktig tid neste morgen.
Hvis vi kaller tiden fra man står opp den første og andre dagen for og Δt=v0+u1, kan våkentiden v0 regnes ut slik:
Med søvnbehov S=7 timer, søvnkonserveringsfaktor α=0.3 og tidsforskjell -6 timer skal man være våken 22 timer og 2 minutter den første natten for å bli uthvilt til rett tid neste morgen.
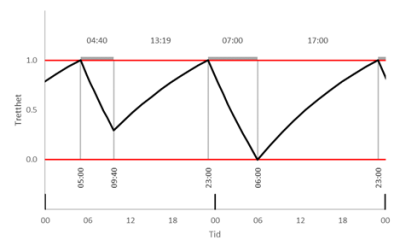
Jetlag øst
Ved reise mot øst viser klokken plutselig et mye senere tidspunkt enn kroppen er forberedt på. Det er ikke lett å sovne til lokal tid første natten, så man bør være oppe til vanlig leggetid hjemme og deretter tilpasse tidspunktet man står opp slik at man blir trett til riktig tid neste natt. Dette tilsvarer situasjonen med dagen etter en fest over, med φ0 = 1. Hvis vi kaller tiden fra man legger seg den første og andre natten for Δt=u1+v1, kan sovetiden u1 regnes ut slik:
Med søvnbehov S=7 timer, søvnkonserveringsfaktor α=0.3 og tidsforskjell +6 timer skal man sove 4 timer og 40 minutter den første natten for å bli trett til riktig tid neste kveld.
Middagshvil
Siden søvnkurven er brattest ved begynnelsen av søvnen, får man mest ut av de første timene med søvn. For å øke våkentiden i løpet av et døgn, kan man sove litt mindre om natten og heller legge inn en kortere middagslur i løpet av dagen. Størst reduksjon av trettheten får man jo senere på dagen man hviler, men siden produktiviteten er størst ved lav tretthet, kan det være bedre å legge middagsluren midt på dagen.