Forskjell mellom versjoner av «Sosialitet»
m |
m |
||
| Linje 16: | Linje 16: | ||
Integralet av det inverse kvadratet av avstanden mellom personene over et døgn gir sosialiteten. Dette er gjennomsnittlig daglig sosialitet. Det er også mulig å beregne momentan sosialitet, men gjennomsnittlig daglig sosialitet er anvendelig og allment akseptert. | Integralet av det inverse kvadratet av avstanden mellom personene over et døgn gir sosialiteten. Dette er gjennomsnittlig daglig sosialitet. Det er også mulig å beregne momentan sosialitet, men gjennomsnittlig daglig sosialitet er anvendelig og allment akseptert. | ||
| − | + | <m> | |
| + | S=\int_{t=0}^{t=\infty}\frac{dt}{r^{2}} | ||
| + | </m> | ||
== Sosialitet med flere aktører == | == Sosialitet med flere aktører == | ||
| Linje 24: | Linje 26: | ||
Med superposisjon kan sosialitetsformelen skrives slik: | Med superposisjon kan sosialitetsformelen skrives slik: | ||
| − | + | <m> | |
| + | S=\underset{i=1}{\overset{N}{\sum}}\int_{t=0}^{t=\infty}\frac{dt}{r_{i}^{2}} | ||
| + | </m> | ||
=== Personer med ulik bølgelengde === | === Personer med ulik bølgelengde === | ||
| Linje 34: | Linje 38: | ||
I analogi til en fjærbelastet kloss med friksjon kan det vises at det sosiale utslaget vil variere av frekvensen og dempingen. Dette kan også skrives om til en funksjon av relativ frekvens i forhold til egenfrekvensen og dempning i forhold til kritisk dempning. Da får vi en korreksjonsfaktor som tar hensyn til de ulike frekvensene. | I analogi til en fjærbelastet kloss med friksjon kan det vises at det sosiale utslaget vil variere av frekvensen og dempingen. Dette kan også skrives om til en funksjon av relativ frekvens i forhold til egenfrekvensen og dempning i forhold til kritisk dempning. Da får vi en korreksjonsfaktor som tar hensyn til de ulike frekvensene. | ||
| − | + | <m> | |
| + | K=\frac{F_{0}}{\sqrt{\left(k-m\omega^{2}\right)^{2}+\left(c\omega\right)^{2}}}=\frac{F_{0}/k}{\sqrt{\left(1-\beta\right)^{2}+\left(2\zeta\beta\right)^{2}}} | ||
| + | </m> | ||
| + | |||
| + | <m> | ||
| + | C=\frac{K}{F_{0}/k}=\frac{1}{\sqrt{\left(1-\beta\right)^{2}+\left(2\zeta\beta\right)^{2}}} | ||
| + | </m> | ||
| + | |||
| + | <m> | ||
| + | \zeta=\frac{c}{c_{k}} | ||
| + | </m> | ||
| + | |||
| + | <m> | ||
| + | \beta=\frac{\omega}{\omega_{e}} | ||
| + | </m> | ||
| + | |||
| + | <m> | ||
| + | \omega_{e}=\sqrt{\frac{k}{m}} | ||
| + | </m> | ||
| + | |||
| + | <m> | ||
| + | c_{k}=2\sqrt{km}=2m\omega_{e} | ||
| + | </m> | ||
| + | |||
Til høyre vises et plott av utslagsvariasjonen avhengig av disse variablene. Grafen viser at utslaget er størst når 2. personens sosioner har omtrent samme frekvens som 1. personens. Vi ser også at selv lave frekvenser vil gi et visst utslag, mens responsen går mot null ved høye frekvenser. | Til høyre vises et plott av utslagsvariasjonen avhengig av disse variablene. Grafen viser at utslaget er størst når 2. personens sosioner har omtrent samme frekvens som 1. personens. Vi ser også at selv lave frekvenser vil gi et visst utslag, mens responsen går mot null ved høye frekvenser. | ||
Revisjonen fra 19. apr. 2012 kl. 20:09
Du trodde kanskje at du visste hva det ville si å være sosial? Men vet du egentlig hva det innebærer? Nei, det gjør du ikke.
Generelt
Enheten for sosialitet er persontimer per kvadratmeter per døgn, eller ph/m2d. Dette kan enkelt eksemplifiseres ved at hvis du har en person på én meters avstand hele døgnet, har du en sosialitet på 24 ph/m2d.
Den fysiske forklaringen på denne måten å beregne sosialitet på, baserer seg på at ethvert menneske sender ut sosiale partiker, såkalte sosioner (eksistensen av sosioner er ennå ikke bevist). Som med annen punktutstråling avtar konsentrasjonen av sosioner med kvadratet av avstanden. Siden sosionene ennå ikke er observert, kjenner man ikke antallet sosioner en person utstråler.
Avstanden som inngår i beregningen av sosialitet er altså avstanden mellom to personer. All den tid sosionene stråler fra hele menneskekroppen og absorberes i kontakt med den andre personen er det vanskelig å operere med en eksakt avstand. Avstanden mellom personenes massesenter kan benyttes som tilnærming, men dette åpner for en uendelighetsproblematikk i tilfellet da massesentrene sammenfaller, slik at man må dele på null.
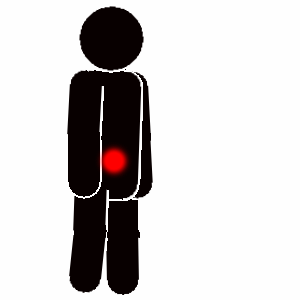
For å unngå uendelighetsproblematikken defineres begrepet personsenter. Personsenteret er definert som massesenteret i oppreist tilstand (se illustrasjon). For en vanlig person befinner personsenteret seg i den øvre mageregionen, men dette varierer med kjønn, alder og kroppslige variasjoner. For tabeller, se NS-EN-1742 Sosialitet - Bestemmelse av personsenter.
Integralet av det inverse kvadratet av avstanden mellom personene over et døgn gir sosialiteten. Dette er gjennomsnittlig daglig sosialitet. Det er også mulig å beregne momentan sosialitet, men gjennomsnittlig daglig sosialitet er anvendelig og allment akseptert.
<m> S=\int_{t=0}^{t=\infty}\frac{dt}{r^{2}} </m>
Sosialitet med flere aktører
I kontakt med flere mennesker vil sosialiteten øke. I små menneskemengder antar vi at superposisjon gjelder, slik at enkeltutslagene kan summeres. Når utslagene derimot blir store, enten i kontakt med mange mennesker eller i intenst sosialt samvær, kan ikke sammenhengen lenger antas å være lineær. Tabellverk og empiriske formler gir mulighet for å beregne sosialiteten i slike tilfeller også.
Med superposisjon kan sosialitetsformelen skrives slik:
<m> S=\underset{i=1}{\overset{N}{\sum}}\int_{t=0}^{t=\infty}\frac{dt}{r_{i}^{2}} </m>
Personer med ulik bølgelengde
Til nå har vi bare betraktet sosiale relasjoner med aktører på samme bølgelengde. Men som fotoner kan sosioner ha ulikt energiinnhold, og det sosiale utslaget er sterkt avhengig av sosionfrekvensen.
I analogi til en fjærbelastet kloss med friksjon kan det vises at det sosiale utslaget vil variere av frekvensen og dempingen. Dette kan også skrives om til en funksjon av relativ frekvens i forhold til egenfrekvensen og dempning i forhold til kritisk dempning. Da får vi en korreksjonsfaktor som tar hensyn til de ulike frekvensene.
<m> K=\frac{F_{0}}{\sqrt{\left(k-m\omega^{2}\right)^{2}+\left(c\omega\right)^{2}}}=\frac{F_{0}/k}{\sqrt{\left(1-\beta\right)^{2}+\left(2\zeta\beta\right)^{2}}} </m>
<m> C=\frac{K}{F_{0}/k}=\frac{1}{\sqrt{\left(1-\beta\right)^{2}+\left(2\zeta\beta\right)^{2}}} </m>
<m> \zeta=\frac{c}{c_{k}} </m>
<m> \beta=\frac{\omega}{\omega_{e}} </m>
<m> \omega_{e}=\sqrt{\frac{k}{m}} </m>
<m> c_{k}=2\sqrt{km}=2m\omega_{e} </m>
Til høyre vises et plott av utslagsvariasjonen avhengig av disse variablene. Grafen viser at utslaget er størst når 2. personens sosioner har omtrent samme frekvens som 1. personens. Vi ser også at selv lave frekvenser vil gi et visst utslag, mens responsen går mot null ved høye frekvenser.
De ulike grafene i figuren viser det vi til nå har omtalt som dempning. Det illustrerer ulike personers evne til å få sosial respons fra et bredt spekter av sosionfrekvenser. Mennesker med lite dempning vil kunne få uhemmede sosiale utslag i nærkontakt med personer i samme frekvensområde. En annen observasjon er at høy dempning medfører en forflyting av maksutslaget mot lavere frekvenser. Det kan tolkes som at de som er tolerante for ulike frekvenser vil legge seg på et lavere frekvensnivå.
Basert på teoriene til Professor Empirator Simen Kjærås.