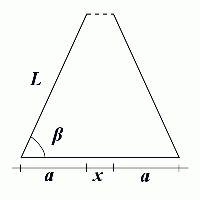Forskjell mellom versjoner av «Pikant»
m |
m |
||
| Linje 19: | Linje 19: | ||
Vikelen ''α'' er da halvparten av en full sirkel delt på ''n'', eller målt i [[radianer]]: | Vikelen ''α'' er da halvparten av en full sirkel delt på ''n'', eller målt i [[radianer]]: | ||
| − | + | <m> | |
| + | \alpha=\frac{1}{2}\frac{2\pi}{n}=\frac{\pi}{n} | ||
| + | </m> | ||
Lengden ''u'' defineres av forholdet: | Lengden ''u'' defineres av forholdet: | ||
| − | + | <m> | |
| + | \mathrm{tan}\,\alpha=\frac{L/2}{u} | ||
| + | </m> | ||
Arealet av den fremkommende trekanten er: | Arealet av den fremkommende trekanten er: | ||
| − | + | <m> | |
| + | \frac{1}{2}u\frac{L}{2}=\frac{1}{4}uL | ||
| + | </m> | ||
Siden det er 2''n'' slike trekanter i mangekanten er det totale arealet 2''n'' ganger dette arealet. | Siden det er 2''n'' slike trekanter i mangekanten er det totale arealet 2''n'' ganger dette arealet. | ||
| Linje 33: | Linje 39: | ||
Da er det totale arealet: | Da er det totale arealet: | ||
| − | + | <m> | |
| + | A=2n\cdot\frac{1}{4}uL=2n\cdot\frac{1}{4}\frac{L/2}{\mathrm{tan}\,\alpha}L=n\frac{1}{4}\mathrm{cot}\,\alpha L^{2}=\frac{n}{4}\mathrm{cot}\,\frac{\pi}{n}L^{2} | ||
| + | </m> | ||
Arealet av en pikant får vi ved å sette ''n'' lik ''π'': | Arealet av en pikant får vi ved å sette ''n'' lik ''π'': | ||
| − | + | <m> | |
| + | A=\frac{\pi}{4}\mathrm{cot}\,\frac{\pi}{\pi}L^{2}=\frac{\pi}{4}\mathrm{cot}\,1\cdot L^{2}\approx 0.504298 L^{2} | ||
| + | </m> | ||
=== Den åpne siden === | === Den åpne siden === | ||
| Linje 45: | Linje 55: | ||
[[Image:Geometri3.gif|200px]] | [[Image:Geometri3.gif|200px]] | ||
| − | + | <m> | |
| + | \beta=\pi-2 | ||
| + | </m> | ||
| − | + | <m> | |
| + | \mathrm{cos}\,\beta=\frac{a}{L}\Rightarrow a=L\,\mathrm{cos}\,\beta | ||
| + | </m> | ||
| − | + | <m> | |
| + | x=L-2a=L-2L\,\mathrm{cos}\,\beta=L\left(1-2\,\mathrm{cos}\,\beta\right)=L\left(1-2\,\mathrm{cos}\,\left(\pi-2\right)\right)\approx 0.1677 L | ||
| + | </m> | ||
* Enkelte matematikere mener at en pikant egentlig er en tredimensjonal figur som er projisert inn i ''xy''-planet. | * Enkelte matematikere mener at en pikant egentlig er en tredimensjonal figur som er projisert inn i ''xy''-planet. | ||
Revisjonen fra 19. apr. 2012 kl. 14:46
Du trodde kanskje at pikant var et adjektiv og betydde skarp eller pirrende? Det er fullstendig galt. En pikant er en geometrisk figur med π (pi) antall kanter.
Geometrisk tolkning
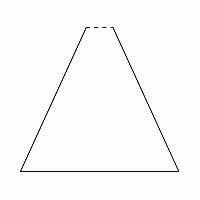
Geometrisk er en pikant en trekant som er litt åpnet, men ikke så mye at den har blitt en firkant.
Omkrets
Omkretsen av en generell n-kant med sidelengde L er nL. En pikant har omkrets πL.
Areal
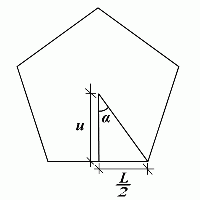
I en generell regulær mangekant med sidelengde L kan vi definere vinkelen α som vist på figuren. Vi definer så lengden u som avstanden fra figurens sentrum vinkelrett på midtpunktet til sidekanten.
Vikelen α er da halvparten av en full sirkel delt på n, eller målt i radianer:
<m> \alpha=\frac{1}{2}\frac{2\pi}{n}=\frac{\pi}{n} </m>
Lengden u defineres av forholdet:
<m> \mathrm{tan}\,\alpha=\frac{L/2}{u} </m>
Arealet av den fremkommende trekanten er:
<m> \frac{1}{2}u\frac{L}{2}=\frac{1}{4}uL </m>
Siden det er 2n slike trekanter i mangekanten er det totale arealet 2n ganger dette arealet.
Da er det totale arealet:
<m> A=2n\cdot\frac{1}{4}uL=2n\cdot\frac{1}{4}\frac{L/2}{\mathrm{tan}\,\alpha}L=n\frac{1}{4}\mathrm{cot}\,\alpha L^{2}=\frac{n}{4}\mathrm{cot}\,\frac{\pi}{n}L^{2} </m>
Arealet av en pikant får vi ved å sette n lik π:
<m> A=\frac{\pi}{4}\mathrm{cot}\,\frac{\pi}{\pi}L^{2}=\frac{\pi}{4}\mathrm{cot}\,1\cdot L^{2}\approx 0.504298 L^{2} </m>
Den åpne siden
Det er vitenskapelige stridigheter om tolkningen av den åpne siden av pikanten. Man vet at den har lengden (π - 3) L ≈ 0.1416 L, men dette strider med at det er en rett linje, siden avstanden mellom de to endepunktene i euklidsk geometri er ≈ 0.1677 L, som vist i det følgende:
<m> \beta=\pi-2 </m>
<m> \mathrm{cos}\,\beta=\frac{a}{L}\Rightarrow a=L\,\mathrm{cos}\,\beta </m>
<m> x=L-2a=L-2L\,\mathrm{cos}\,\beta=L\left(1-2\,\mathrm{cos}\,\beta\right)=L\left(1-2\,\mathrm{cos}\,\left(\pi-2\right)\right)\approx 0.1677 L </m>
- Enkelte matematikere mener at en pikant egentlig er en tredimensjonal figur som er projisert inn i xy-planet.
- Andre hevder at de ekstra 0.0026 L kommer fra luftforurensning i Asia.
- Den åpne siden er også blitt brukt til narkotikasmugling.